Have you ever looked at your shadow in the summer?
Depending on the time of day, the shadow could be longer than you or shorter than you. It is still you - you may look shorter or taller, but everything else is the same. You can say that your shadow is similar to you.
This principle can be applied in identifying similar shapes.
Similar shapes have things in common but one is larger than the other.
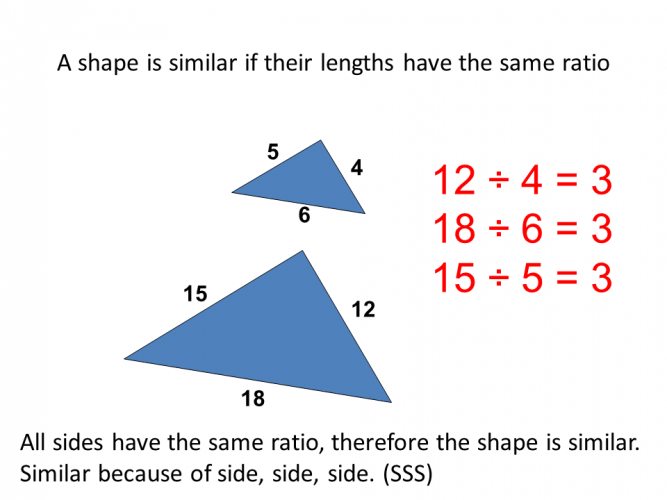
Shapes are similar if their corresponding angles are equal and the corresponding sides are in the same ratio.
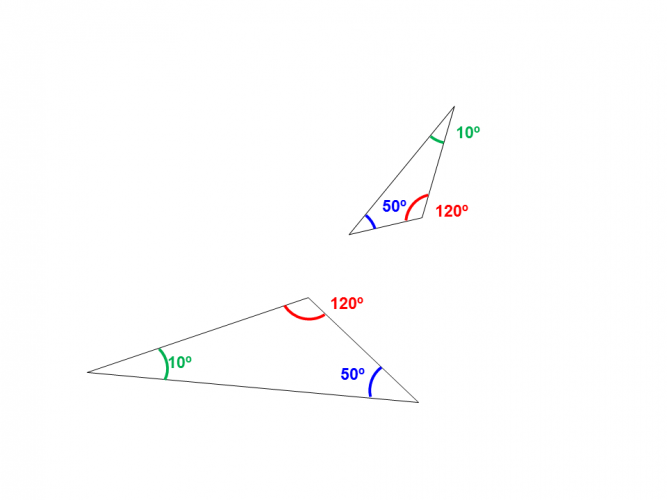
Example 1:
Example 2:
Make sure that when triangles are rotated, the angles still correspond.
You only need to be given two corresponding angles to decide if a shape is similar.
If two corresponding angles are the same, then the third angle must be the same because of the rule that angles in a triangle add up to 180°.
Example 3:
Example 4:
And now over to you to see if you can identify similar shapes.