In this activity, you will calculate angles and lengths within 3D shapes, using your knowledge of trigonometry.
The trig ratios are often combined with Pythagoras when solving problems relating to right angled triangles. This means that these type of questions need to be broken down and solved in stages.
Let's recap the rules that you should be familiar with:
Pythagoras' Theorem
a² + b² = c²
Trig ratios ("SOH CAH TOA")
sin x = O/H
cos x = A/H
tan x = O/A
How do we combine these two sets of rules to work in 3D?
Let's have a look at the method with an example.
Example question
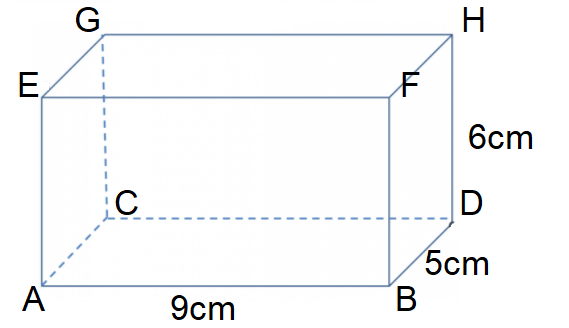
Shown below is cuboid ABCDEFGH.
AB = 9cm
BD = 5cm
DH = 6cm
Calculate angle AHD.
Step 1: Sketch the shape and label the lengths if they are not already written down.
Step 2: Create a right-angled triangle on the base of the shape and use Pythagoras to work out the diagonal length.
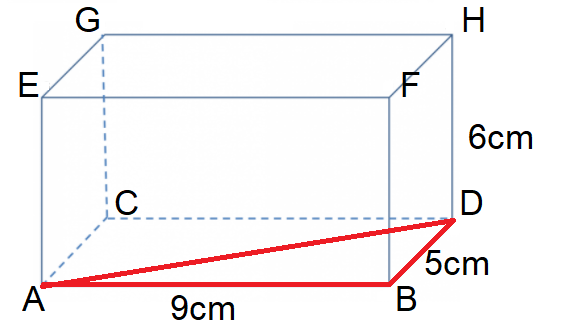
Shown in red is right-angled triangle ABD. AB = 9cm, BD = 5cm, AD = hypotenuse.
Substituting and rearranging Pythagoras, we get:
AD = √(52 + 92)
AD = √106
Step 3: Create another right-angled triangle through the shape. If you are working out an angle, use the correct trig ratio to solve.
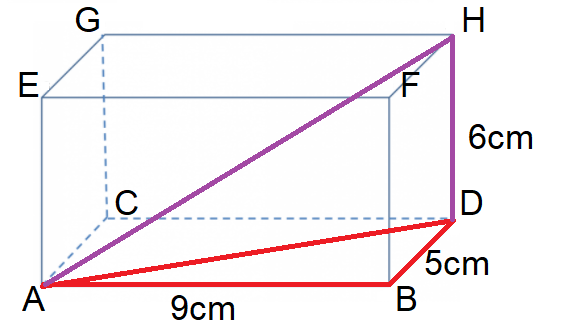
Shown in purple is right-angled triangle ADH. This new triangle shares a length with the triangle from Step 2, meaning you can use your answer from the previous step.
AD = √106cm, DH = 6cm
We have drawn this triangle because the question wants us to calculate angle AHD. DH is adjacent to the angle and AD is opposite.
As we have an adjacent and an opposite length, we need to use tan to solve.
tan x = O/A
tan x = √106 / 6
x = tan-1 (√106 / 6)
x = 59.8º (1 d.p.)
And that is how to combine Pythagoras with trig ratios to find an angle in a 3D shape!
The key point is to sketch the shape, and draw the lines inside that you need to find the angle or length. Once you start to look at the shapes as individual right-angled triangles, it just becomes a case of applying Pythagoras or "SOH CAH TOA".
Have a go at the activity and see if you can apply these skills!