Find the Surface area of a Pyramid

Question: Why don't mummies go away on holiday?

Answer: They are afraid that they will relax and unwind.

 

This is a clue to our topic.

We are going to look at the surface area of pyramids.

The surface area of a pyramid is the area of each face of the pyramid added together. Let's look at how we do this using an example.

 

 

Example 1:

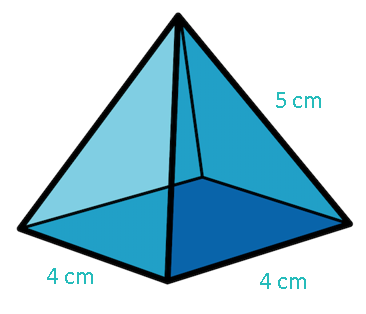
This pyramid has a square base with a side length of 4 cm and its edge length (the length connecting each corner of the base to the pyramid's point) is 5 cm.

The simplest way to think about the surface area of a pyramid is to picture its net:

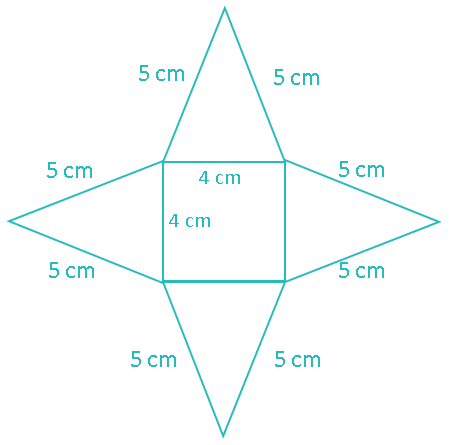
This pyramid has five faces; its square base and four identical triangular faces. 

The area of the base is 4 x 4 = 16 cm² 

But what about the area of the triangular faces? The area of a triangle is equal to base x height ÷2, so we need to know the height of the triangles.

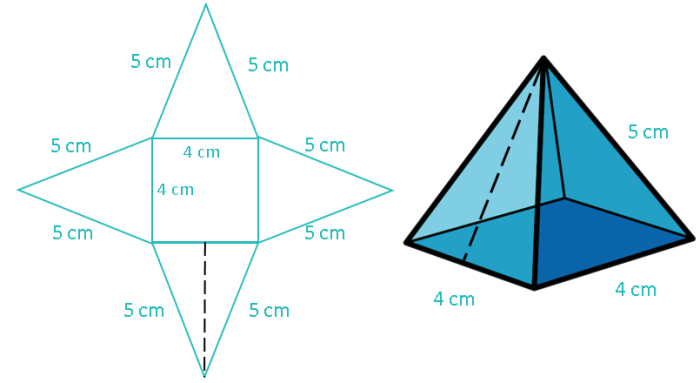
This height, marked on the net and the pyramid above, is called the slant height of the pyramid. It joins the centre of the side of the base with the pyramid's point. To work this length out, we need to recognise that this line forms a right-angled triangle with the side of the pyramid's base and its edge:

 

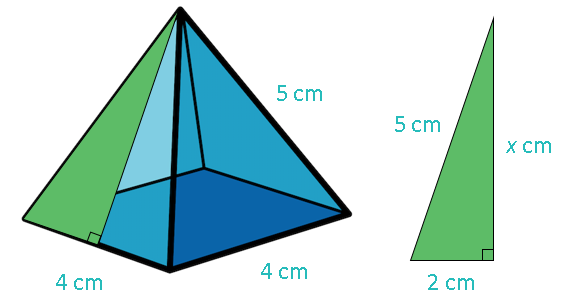
The hypotenuse of this right-angled triangle is the edge of the pyramid, which is 5 cm long. One of the shorter sides is half the length of the side of the pyramid's base, which is 2 cm, and the other shorter side is the length we want to calculate. We can calculate x using Pythagoras' Theorem:

 

x² + 2² = 5²

x² + 4 = 25

x² = 21

x =√21 = 4.58257...

x = 4.58 (to 2 decimal places)

Now we can find the area of each of the triangular faces.

Remember, the area of a triangle is base x height ÷ 2, so:

Area of each triangular face = 4 x 4.5825... ÷ 2 = 9.1651... cm²

 

Finally, add all the areas together:

Total surface area = area of base + 4 x area of triangle

                          = 16 + 4 x 9.1651...

                          = 52.6606...cm²

The total surface area is 52.7 cm² (to 1 decimal place).

 

Top Tip! Using exact values throughout prevents any rounding errors in your final answer.

 

 

Example 2:  

Find the surface area of this square-based pyramid:

 

Don't panic - you've got this!

First you need to need to apply Pythagoras' Theorem to find the slant height of the pyramid:

The right-angled triangle you need has a hypotenuse of 9 cm (the edge of the pyramid), and a shorter side of length 3.5 cm (half the length of the side of the pyramid's base). By Pythagoras' Theorem:

 

x² + 3.5² = 9²

x² + 12.25 = 81

x² = 68.75

x = √68.75 = 8.2915... cm

 

Now you can find the surface area:

1. Calculate the area of the base: 7 x 7 = 49 cm²

2.  Calculate the area of each triangular face: 7 x 8.291... ÷ 2 = 29.020... cm² 

3.  Multiply the area of the triangle by four as there are four identical triangular faces:  29.020... x 4 = 116.081... cm²

4.  Add the areas of the base and the four triangles together: 49 + 116.081...  = 165.081... cm²

The total surface area is 165.1 cm² (to 1 decimal place).

 

Phew! One final example to look at, and this one's a little trickier...

 

Example 3:

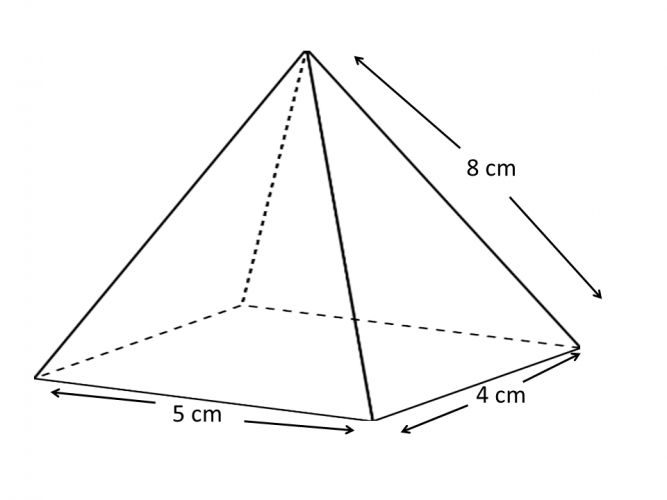
Find the area of this rectangular-based pyramid:

 

This is a little different, so be careful. The base of the pyramid is a rectangle, rather than a square, which means that the four triangles are not all identical. In fact the pyramid has two different slant heights; one down the middle of the triangular faces with base 5 cm, and one down the middle of the triangular faces with base 4 cm:

 

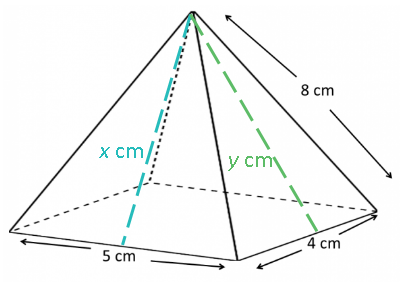
We need to apply Pythagoras' Theorem twice to calculate the two slant heights.

For the triangle with base 5 cm:

x² + 2.5² = 8²

x² + 6.25 = 64

x² = 57.75

x = √57.75 = 7.599... cm

 

For the triangle with base 4 cm:

y² + 2² = 8²

y² + 4 = 64

y² = 60

y = √60 = 7.745...... cm

 

 

Now we can find the surface area:

1. Base: 5 x 4 = 20 cm²

2. Triangle with base of 5 cm: 5 x 7.599... ÷ 2 = 18.998...cm²

3. Triangle with base of 4 cm: 4 x 7.745... ÷ 2 = 15.491...cm²

4. There are two of each triangle, so the total surface area is 20 + 2 x 18.998... + 2 x 15.491... = 88.980...cm²

The total surface area is 89.0 cm² (to 1 decimal place).

Remember, using exact values throughout prevents any rounding errors in your final answer.

 

Got all that? Time to try some questions...