Use Angle Properties Around a Point

 

Have you ever wondered about the maths that makes a fairground work?

When you are on a fast ride, trying not to scream, you may think to yourself, "I really hope the designer got the angle measurements correct here!"

 

Angles are all around us, everywhere.

We may not often think about them, but rather just trust that engineers and designers have got this element right. 

 

In this activity, we are going to investigate angles around a point.

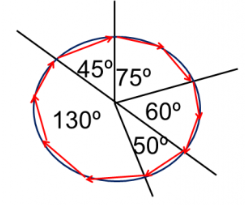
The key fact to remember is that angles positioned around a point always add up to 360°.

If they don't, then sack the designer!

 

 

Let's see this fact in action in an example now.

Angles around a point add up to 360°

 

 

45° + 75° + 60° + 130° + 50° = 360°

So how do we use this information to help us find the value of an unknown angle? 

e.g. What is the value of the angle j in the diagram below?

 

 

Firstly, we need to add up the value of the angles provided:

105° + 110° + 48° = 263°

 

Then we can subtract this amount from 360° to find the value of the unknown angle:

 360° - 263° = 97°

It's as simple as that.

 

Now let's take our newfound skills for a spin.

In this activity, we will use the key fact, that angles around a point always add to 360°, to find the value of unknown angles using numbers and algebra and solve problems involving collections of angles.