.jpg)

Oh yes, the humble triangle, we take it for granted.
Its shape has been used by Egyptian kings, musicians and in warning signs, to name just a few of its many uses!
There are lots of properties (facts) about triangles that people have learned over the centuries, and now it is your turn.
Special Triangles
From left to right:
An equilateral has 3 equal sides
An isosceles has 2 equal sides
A scalene has no equal sides.
We need to look out for the markings on these triangles, as these tell us which type of triangle we are looking at.
We also need to remember the rules about angles in each type of triangle:
All three angles in an equilateral are equal.
The two angles at the base of an isosceles are equal.
All three angles in a scalene are different.
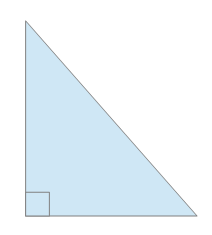
Finally, any triangle containing a 90 degree angle is called a right-angled triangle.
Right-angled triangles can be scalene or isosceles, but not equilateral.
A Key Triangle Fact:
Angles in a triangle always add up to 180°.
Using this knowledge, we can find missing angles in a triangle.
Let's look at how we can do this now.
e.g. What are the value of angles a and b in the triangle below?
From the markings on these triangles, we can see this is an isosceles triangle.
As a result, we know that the base angles must be the same.
Therefore, b = 70º
Finally, angles in a triangle add to 180º, so angle a = 180 - 70 - 70 = 40º
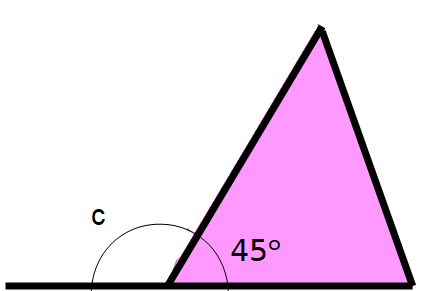
e.g. What is the value of angle c in the diagram below?
Here, we have been asked to find an angle that is external to the triangle.
We need to put two rules we know together here - if we extend the base of the triangle we have a straight line.
What facts do we know about straight lines?
The angles on a straight line will also add up to 180°, so we can use this fact to find the missing exterior angle.
So angle c = 180 - 45 = 135º
Right then, let's put what we know into action now!
In this activity, we will use the key fact, that angles in a triangle always add to 180°, to find the value of unknown angles in triangles, identify triangles accurately and solve problems involving triangles.





.PNG)