Identify the Properties of a Circle

Circles are everywhere around us - how many examples can you think of, or perhaps even see, whilst you are attempting this activity?

 

It is useful to know some fundamental details about circles to help us when we are working with them in geometry.

Think of it as your toolbox of circle knowledge - if you can reach in and choose the correct piece of information to apply to a given problem, you will be able to solve it easily. 

 

Let's start filling your circles toolkit with essential terms and facts now. 

 

 

 

The circumference is the name given to the total distance around the outside of a circle:

 

 

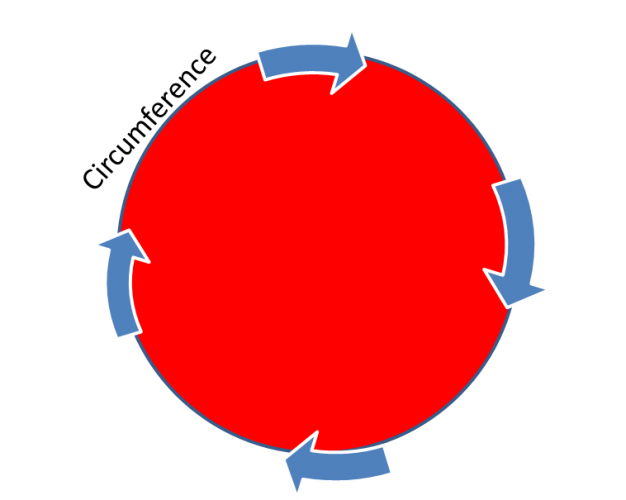
Sometimes it can be referred to as the perimeter also, but this is less common.

 

 

The diameter is the name given to a line that passes directly through the centre of a circle, from one edge to the other:

 

 

 

The radius is a line that passes from the centre of the circle to the edge:

 

 

Top tips: 

If you have been given the radius and want the diameter,  just double the radius;

If you have been given the diameter and want to find the radius, just halve the diameter.

 

 

A chord is the term used to describe a line that passes from one edge of the circle to another, without passing through the centre.

There are three chords in this example:

 

 

When a chord is drawn within a circle, it will split the circle into segments.

The smaller part created is referred to as the minor segment, whilst the larger part is the major segment.

 

 

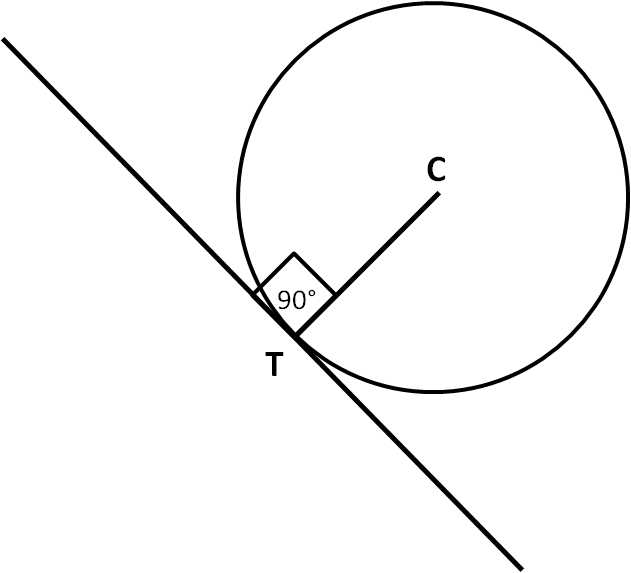
A tangent is a line that hits the edge of a circle at right angles to the radius:

 

 

 

 

Sometimes circles are cut into sectors, like this pizza:

 

 

Sectors are the area between two radiuses and the connecting arc of a circle, so they must originate in the centre.

The slice is the minor sector and the rest is the major sector.

 

 

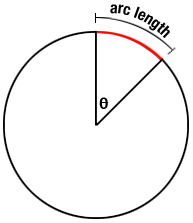
An arc is the part of the circle that forms the outer, curved edge of a sector:

 

 

 

When working with circles, we need to keep two essential numbers and associated facts in mind:

1) There are 360° degrees in a circle (or around a point); 

2) Many circle calculations will employ the use of the constant 'pi' (π) which can be rounded to 3.142. There is a special button for this on your calculator so that you don't need to round it and can work with the exact value. It will probably look like this:

 

 

 

 

In this activity, we will apply these definitions, recognise their usage in example circles, and use circle facts to solve related geometric problems. 

 

Let's put your toolkit to work right now!