In geometry, translation simply means moving without rotating, resizing or anything else.
It can be best summed up by the word: slide.
How do we describe a translation?
When we are translating an object, we need to know how far to move it.
We do this by saying how far right or left it needs to move, plus how far up or down it needs to move.
We describe this movement using a vector.
What is a vector?
A vector looks like this:
| a |
| b |
a defines the horizontal movement (left or right) and b defines the vertical movement (up or down).
If a is positive, the movement will be to the right and, if it is negative, it will be to the left.
If b is positive, the movement will be up and, if it is negative, it will be down.
Let's look at some examples:
| 4 | 4 right |
| 5 | 5 up |
| 3 | 3 right |
| -1 | 1 down |
| -2 | 2 left |
| 0 | no vertical movement |
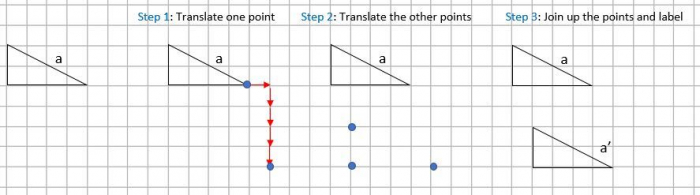
How do we move a shape?
The key thing to remember about translations is that every point of the shape must move the same distance and in the same direction.
So if we move each corner individually by the same distance and in the same direction, then we can rejoin the points and create the new shape.
Let's look at these features and processes in action now in an example.
e.g. Translate shape a by the vector:
| 1 |
| -4 |
This vector means we have to move the shape 1 square to the right and 4 squares down.
Let's put this process into action and try translating some points and shapes now.
In this activity, we will interpret and create vectors then use these to affect translations of points and shapes, as shown in the method above.