Enlarge 2D Shapes

What is enlargement?

 

The word enlargement is usually taken to mean making something bigger.

In geometry, however, it actually means changing the size of a shape or object.

So it can mean either making a shape bigger or making a shape smaller.

 

 

What information do we need to have to enlarge a shape?

 

To enlarge a shape, we need to have a scale factor.

This tells us how many times bigger (or smaller) the shape should become.

 

A scale factor of 2 would mean each side of the shape should be doubled;

A scale factor of 3 would mean each side of the shape should be trebled;

A scale factor of 1/2 or 0.5 would mean each side of the shape should be halved.

 

Let's look at enlargement in action using some examples. 

 

 

 

e.g. A shape is enlarged by a scale factor of 3. If one of the sides in the original shape is 2 cm long, how long will this side be in the enlarged shape?

 

All we have to do here is to multiply the length given by 3:

2 cm × 3 = 6 cm

 

 

 

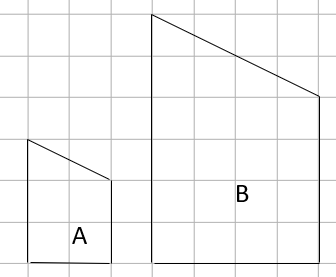
e.g. Shape A has been enlarged to create shape B (see below). What scale factor has been used to create this enlargement?

 

 

Firstly, we need to work out if the enlarged shape is bigger or smaller than the original.

If it is bigger, then the scale factor used will be greater than 1.

If it is smaller, the scale factor used will be between 0 and 1. 

 

In this case, it is bigger, so our scale factor will be a number greater than 1.

 

Now, we need to compare a pair of sides of the shapes - one from the original and one from the enlargement.

It doesn't matter which pair we choose, so long as they match, as they will all give the same answer.

 

If we look at the left-hand vertical edge of each shape, it is 3 squares tall in shape A and 6 squares tall in shape B.

 

This means that the scale factor used is 2, as 6 ÷ 3 = 2. 

 

 

 

e.g. Shape B has been enlarged to create shape A (see below). What scale factor has been used to create this enlargement?

 

 

Firstly, we need to work out if the enlarged shape is bigger or smaller than the original.

In this case, it is smaller, so our scale factor will be a number between 0 and 1.

 

Now, we need to compare a pair of sides of the shapes - one from the original and one from the enlargement.

If we look at the left-hand vertical edge of each shape, it is 3 squares tall in shape A and 6 squares tall in shape B.

 

This means that the scale factor used is 1/2 or 0.5, as 3 ÷ 6 = 0.5. 

 

Can you see how knowing if we are looking for a fractional scale factor or a number greater than 1 helps us to know which way round to divide? 

 

 

 

In this activity, we will enlarge shapes by given scale factors, determine scale factors after an enlargement has occurred, and use the process and features of enlargements to solve related geometric problems. 

 

Let's get enlarging!