Find a Missing Angle Using the Cos Ratio

You may have used a "SOH CAH TOA" formula triangle to find a missing side of a right-angled triangle.

You can also use them to find the missing angle in a right-angled triangle.

 

Here, we are going to look at the cos formula triangle and how to calculate an angle from it.

Let's remind ourselves of the formula triangle:

 

 

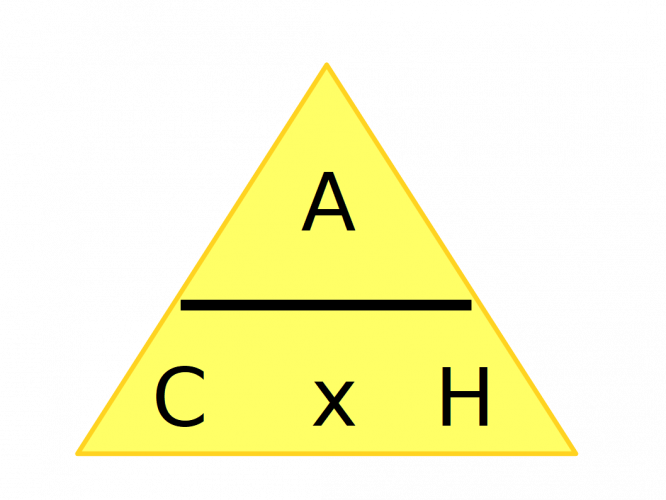
C = cos (of angle)

A = adjacent length

H = hypotenuse

 

The formula is C = A/H. This means:

cos(angle) = A/H

 

You may have used formula this to find an adjacent length or hypotenuse when you had an angle.

 

If you are finding an angle, you substitute the lengths into the same formula - you just need to then use a function known as inverse cos to calculate it (this is written as cos^-1). On most calculators, this is accessed by pressing SHIFT and then cos.

So, the formula for finding an angle with an adjacent and hypotenuse is:

angle = cos^-1(A/H)

 

 

Let's give it a go...

IMPORTANT NOTE: Make sure your calculator is set to degrees. You can tell as a "D" appears at the top of the calculator screen.

 

Example 

Find angle x in this triangle.

 

 

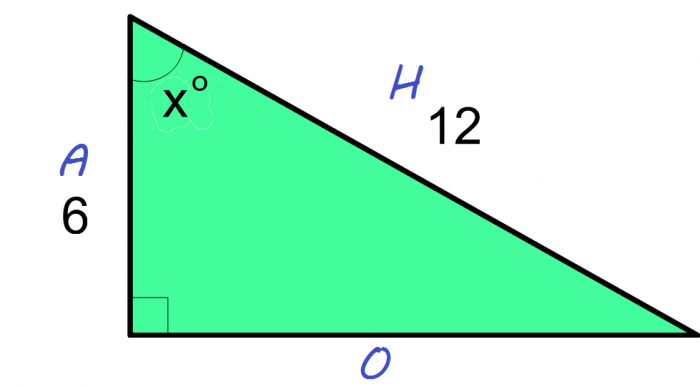
1. Label the triangle. 

 

2. Identify the two sides you want to use. If you want to find the angle using cos, you will need the hypotenuse H, and the length of the adjacent side, A.

 

3. Substitute the lengths into the formula C = A ÷ H to calculate cos x.

6 ÷ 12 = 0.5

cos x = 0.5

 

4. Finally, use the inverse cos button (cos ^-1) on your calculator on this value.

x = cos^-1(0.5) = 60°

 

 

If you follow these steps, you should be able to find the angle in a right angled triangle when you have A and H.

Have a go at this activity and practise this skill!