.jpg)
Did you know that trigonometry can be used to calculate the position from the shore to a ship?
The person on the shore can find the angle between the shore and the ship and the ship's captain can find the angle from the ship to shore. It looks a bit like a pirate ship, so best we can locate their exact position in case we need help!
The sine rule is used to calculate angles in a non-right angled triangle. The formula is:
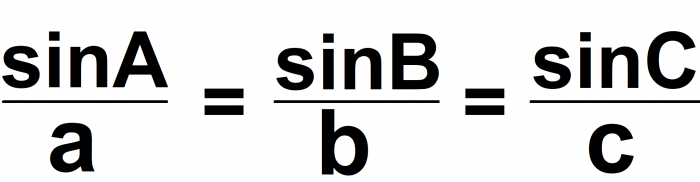
It looks the same as the sine rule for finding a side length. The difference is that the terms have been turned upside down with the angles (sin) being on the top.
You will need a scientific calculator in order to get the sin-1 button. Make sure it is set to degrees.
Example 1
Calculate angle x.
.png)
Step 1: Label the angles of the triangle if it hasn't already been labelled. Our angles are A, B, and C. You are free to pick the order they go in.
.png)
Step 2: Label the lengths. This is where you have to be very precise, otherwise the formula will not work. The length opposite angle A must be called a, the length opposite angle B must be called b, and the length opposite angle C must be called c.
.png)
A = 60°
B = x
C = (blank)
a = 7cm
b = 6cm
c = (blank)
Step 3: Write the formula that you will need. Notice that length c and angle C are both blank, so in this case, we can leave them out:
sin A / a = sin B / b
Step 4: Substitute your known values:
sin 60 / 7 = sin x / 6
Step 5: Rearrange the formula to make sin x the subject:
sin x = 6 x (sin 60 / 7)
sin x = 0.74 ...
Step 6: Use inverse sin ("sin-1") to find the angle. (Just remember to press "shift" + "sin" on your calculator to make it appear).
x = sin-1 (0.74...)
x = 47.9° (to 3 significant figures)
NOTE: If you try to put it all into the calculator at once, the rules of BIDMAS aren't followed and your answer will be incorrect.
Let's give it a try...







