Find an Angle Using the Cosine Rule

Have you ever wondered what it's like to dangle outside of a space station to go to work?

 

 

The robotic arms are operated by controlling the angles of its joints.  Calculating the final position of the astronaut involves trigonometry, one aspect of which is finding angles. So the ability to calculate angles within triangles is one of the skills that astronauts and aerospace engineers need to do their job. 

 

The cosine rule

 

The cosine rule is used to find a length in a non-right angled triangle. 

Suppose you have triangle abc as shown:

 

 

 

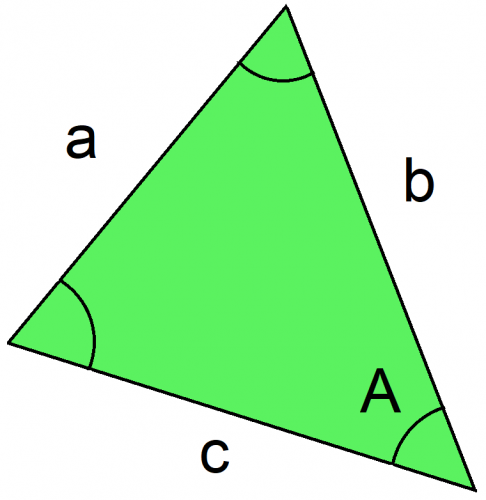
The cosine rule allows you to work out length a with the formula:

a² = b² + c² - 2bc cos A

 

IMPORTANT POINT: When labelling your triangle, it doesn't matter which way round lengths b and c are, but angle A must be opposite length a.

 

Now, this formula can be rearranged for cos A as follows:

cos A = (b² + c² - a²) / (2bc)

 

Notice the use of brackets around the (b² + c² - a²) and (2bc). You should get into the habit of doing this if you are typing it all into your calculator, otherwise it will use BODMAS and give you an incorrect answer. 

 

It's then a case of substituting each length into the formula to find cos A.

Once you have a value for cos A, you then have to use "inverse cos" (cos^-1) to calculate the angle.

 

Think of it this way: You use the cosine rule to find an angle if you know all three lengths of the triangle.

 

Make sure your calculator is set to degrees.

 

 

Example

Calculate angle A.

 

 

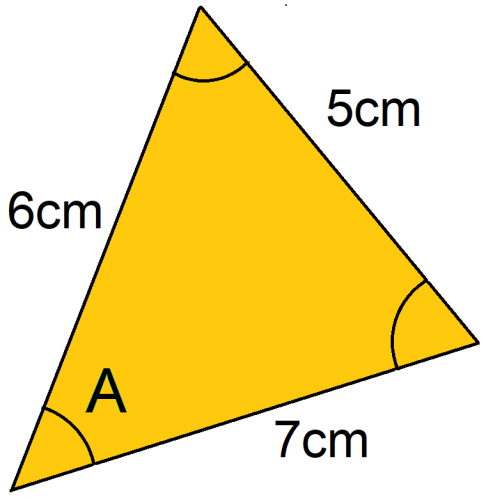
As we can clearly see, this is not a right-angled triangle and we have all three sides given. This means we need to use the cosine rule to find the angle.

 

First, we need to identify each length.

Length a = 5cm, because it is opposite the angle we want to find.

Lengths b and c can be either way round and the formula will still work. 

 

So let's say:

a = 5cm

b = 6cm

c = 7cm

 

Write the formula:

cos A = (b² + c² - a²) / 2bc

 

Substitute the values for a, b, and c:

cos A = (6² + 7² - 5²) / (2x6x7)

cos A = (60) / (84)

cos A = 0.71428... 

 

Now that we have a value for cos A, all we need to do is use inverse cos:

A = cos^-1(0.71428...)

A = 44.4° (1 d.p.)

 

And that is how to use the cosine rule to calculate an angle!

 

TIPS:

- If you have a negative value for cos A, it means that the angle you convert to will be obtuse (i.e over 90°).

- The largest angle in a triangle will always be opposite the longest length.

 

These are a good way to check if your answer is sensible.