Find the Area of Compound Shapes

 

Question: What do you call an alligator in a vest?

Answer: An investigator, of course.

 

Let's investigate how to find the area of compound shapes including circles.

Compound shapes are shapes made up of two or more simple shapes.

All we need is to be able to work out the area of these simple shapes.

Let's recap.

 

 

Area of a square/rectangle/parallelogram = base x height

Area of a triangle = base x height ÷ 2  OR 1/2 base x height

Area of a circle = π x radius x radius (πr²)  

The value of π is usually taken as 3.14 or use the π button on your calculator.

 

 

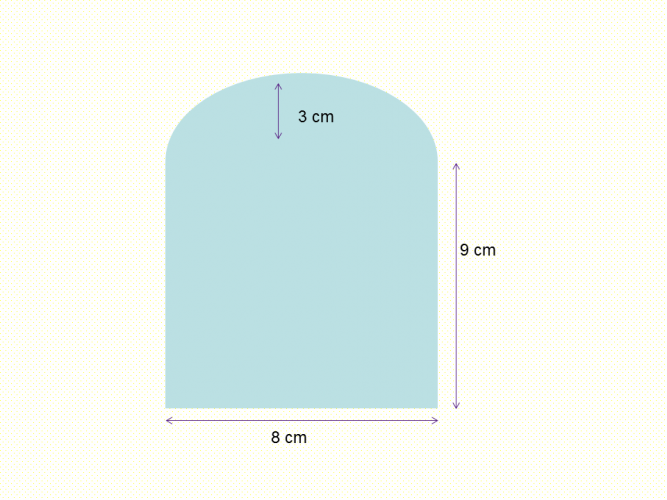
Example 1:

 

 

Here, you can separate this shape into a rectangle measuring 9 cm x 8 cm = 72 cm² and a semicircle.

To find the semicircle, find the area of the full circle: π x 3 x 3 =  28.27 then divide by 2 =  14.14 cm²

Now just add 72 cm² to 14.14 cm² = 86.14 cm²

 

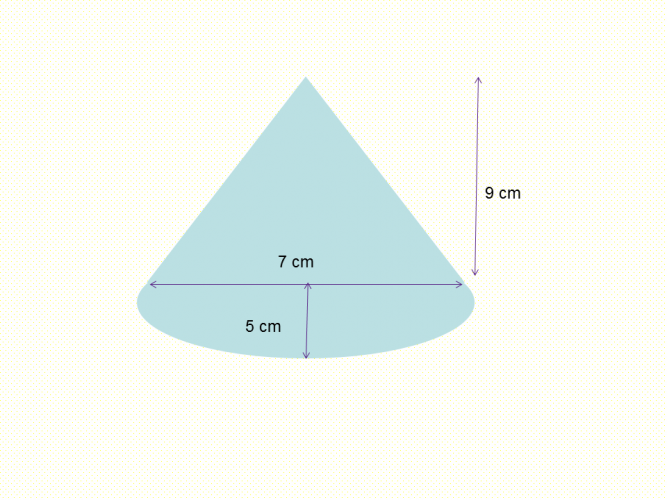
Example 2:

 

 

Area of the triangle: 7 x 9 = 63 cm² ÷ 2 = 31.5 cm²

Area of the semicircle: π x 5 x 5 = 78.54 cm² ÷ 2 = 39.27 cm²

Total area: 31.5 cm² + 39.27 cm² = 70.77 cm²

 

Your turn to investigate.