Did you know it took the Ancient Egyptians 20 years to build one pyramid?
And guess what, someone came along and chopped the top off. The Egyptians must have been really cheesed off.
They soon got over it though as they realised there was another shape to play with and so along came the frustum.
We generally only come across them in our maths studies and are usually asked to find the volume.
Have you heard the song 'New York, New York' it was so good they named it twice.
To find the volume of a frustum, you do the same, you use the formula twice.
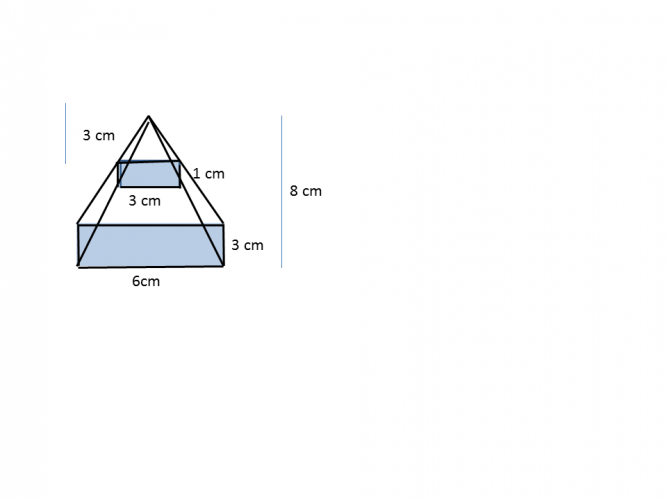
Example 1:
Find the volume of the frustum above
Recap of formula for finding the volume of a pyramid: 1/3 x base area x vertical height - often written as 1/3Ah
Volume is measured in units³
Three simple steps:
1. Calculate the volume of the square-based pyramid.
2. Calculate the volume of the smaller pyramid as shown.
3. Subtract the smaller volume from the larger one.
Base area of the larger pyramid: 6 x 3 = 18 cm²
Volume: 1/3 x 18 x 8 = 48 cm³
Base area of the smaller pyramid: 3 x 1 = 3 cm²
Volume: 1/3 x 3 x 3 = 3 cm³
Volume of the frustum: 48 - 3 = 45 cm³
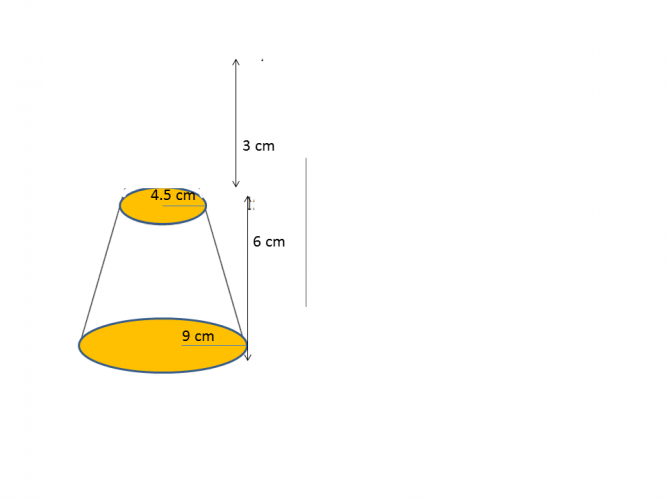
Example 2:
Find the volume of the frustum above
Recap of formula for the volume of a cone: 1/3 x π x r² x h
Base area of large cone: π x r² = 254.47 cm² (correct to 2 decimal places)
Volume of a full cone: 1/3 x 254.47 x 9 = 763.41 cm³
Base area of the smaller cone: π x r² = 63.62 cm² (correct to 2 decimal places)
Volume of the smaller cone: 1/3 x 63.62 x 3 = 63.62 cm³
Volume of the frustum: 763.41 - 63.62 = 699.79 cm³
In the following activities, the π button has been used on the calculator.
For 1/3 1 ÷ 3 has been used.
Round to two decimal places as you work through each part.