Identify Reflective Symmetry

What is reflective symmetry?

 

Reflective symmetry is when a shape or pattern is reflected in a line of symmetry or a mirror line.

The reflected shape will be exactly the same as the original, the same distance from the line of symmetry and the same size.

 

 

What is a line of symmetry?

 

Lines of symmetry are imaginary lines that can be drawn on two-dimensional shape, where the image on either side of the line matches exactly. 

Where lines of symmetry are drawn on shapes, they are usually represented as a dashed line. 

 

 

 

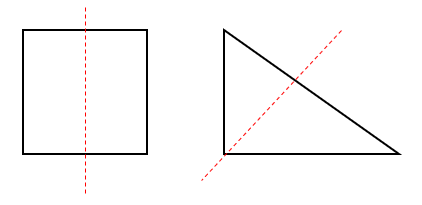
e.g. Are these lines of symmetry?

 

 

Imagine that we could fold the square along the dashed line - would both halves of the shape fit perfectly over each other?

 

If so, then we have a line of symmetry.

In the case of the square, they do perfectly match, so the line of symmetry shown here is correct.

 

With the triangle, the shapes on either side of the line are not the same.

Can you see that the triangle on the left of the line is smaller than the one on the right? 

So, the line of symmetry shown on the triangle is not correct.

 

 

 

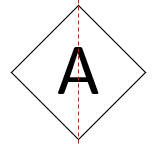
e.g. How many lines of symmetry does the following shape have?

 

 

This has shape two elements - the outer square and the letter A.

A square has 4 lines of symmetry, whilst the letter A has 1 line of symmetry.

 

When we have two elements present, the lowest number of lines of symmetry is the one we need to use.

 

So in this case, we have one line of symmetry on the combined shape, shown here:

 

 

 

 

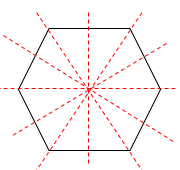
e.g. How many lines of symmetry does the following shape have?

 

 

This example is actually easier than the last one.

This is a regular hexagon; remember that 'regular' means all the angles and sides are the same.

 

When we have a regular shape, the number of lines of symmetry is the same as the number of sides present, so this shape has 6 lines of symmetry, shown here:

 

 

 

 

In this activity, we will identify valid lines of symmetry and define if and where they occur in a range of regular and irregular shapes. We will also use the logic that the number of lines of symmetry match the number of sides present to solve related problems.